[Project_하다]/[Project_공부]
[CS231n] #4. Neural Network
브렌쏭
2024. 7. 1. 14:57
경사하강, Gradient Descent
| Calculation Speed | Proximity | Level | |
| Numerical gradient | slow 😢 | approximate 😢 | Easy to Write 🤩 |
| Analytic gradient | F A S T 🤩 | Exact 🤩 | error-prone 😢 |
So, Analytic gradient is better
어쨌든 확률 + 표본을 통한 해석적 경사하강법을 이용하는 것이 효율적이다.
함수가 복잡해지면 복잡해질수록 각 표본이 기하급수적으로 늘어나므로 훨씬 이득이라고 할수있으며, 최신 방식을 일일히 경사하강법으로 구하고 있다면 연산량이 너무 많아진다.
Back Propagation : 역전파

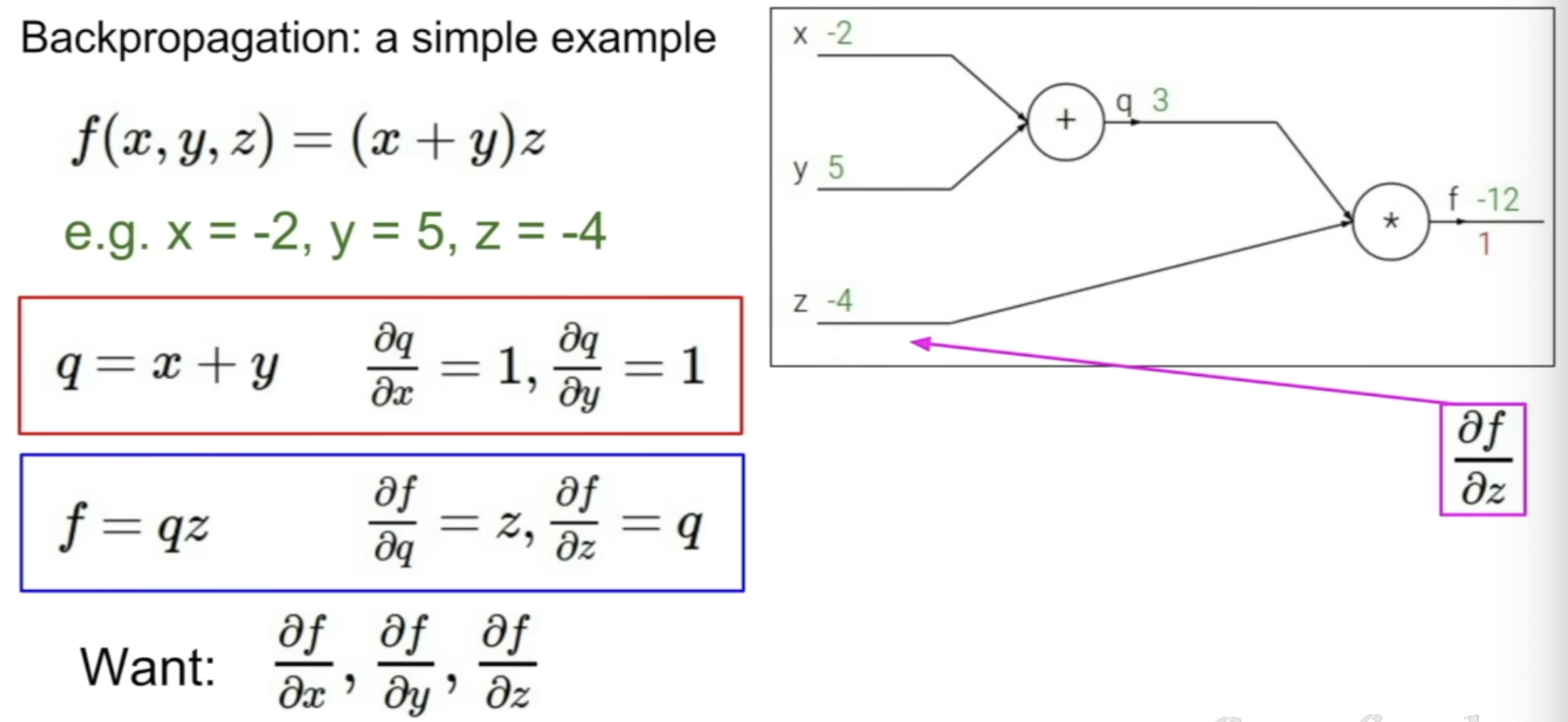
- 함수에 대한 computational graph를 제작한다
- 각 local gradient를 구한다
- chain rule을 이용한다
- z에 대한 최종 loss L은 이미 계산되어 있음을 이용한다
- 목표는 input에 대한 gradient를 구하는 것이다
# f(x, y, z) = (x + y) * z
# q = x + y
# 1. df/dq
f = q * z
df/dq = z = -4
# 2. df/dz
f = q * z
df/dz = q = 3
# 3. df/dx
q = x + y
dq/dx = 1
df/dx = df/dq * dq/dx = -4 * 1 = -4
# 4. df/dy
q = x + y
dq/dy = 1
df/dy = -4
스스로 이걸 이해하고 쓰고 있는건지 의구심이 들기 시작했다.
기반 지식을 다른 곳에서 좀더 쌓아야 할거 같은 느낌