Tags
- 카페
- 사진
- CS231n
- fdr-x3000
- 전시
- 오사카
- 축복이
- 여행
- 우리fis아카데미
- 제주도
- SQL
- 대만
- 시청
- 대만여행
- 수요미식회
- 17-55
- 650d
- ai_엔지니어링
- k-디지털트레이닝
- 해리포터
- 전주
- 축복렌즈
- 우리fisa
- 글로벌소프트웨어캠퍼스
- 맛집
- 건담
- 우리에프아이에스
- Python
- 군산
- 도쿄
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Today
- Total
Recent Posts
300x250
브렌쏭의 Veritas_Garage
[BoostCourse] 확률론 본문
딥러닝과 확률론
이전에 언급했던 Loss function 은 L1, L2 Norm의 공식을 이용한다.
- 회귀분석에서 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도 (L2 Norm)
- 분류문제에서는 교차엔트로피를 사용하여 모델예측의 불확실성을 최소화하는 방향으로 학습을 유도한다.
확률분포 : 데이터의 초상화
- 데이터 공간은 x * y 라고 표기하고 D는 데이터 공간에서 데이터를 추출하는 분포
- 데이터는 확률변수로 (x, y)~D 라고 표기
이산확률변수 VS 연속확률변수
- Discrete: 이산형
- Continuous: 연속형
각 데이터 공간으로 인해 결정되는 것이 아니다.
확률 분포의 종류에 따라 결정되는 것.
이산확률변수
확률변수가 가질 수 있는 모든 경우의 수를 고려해 확률을 더해서 모델링한다.
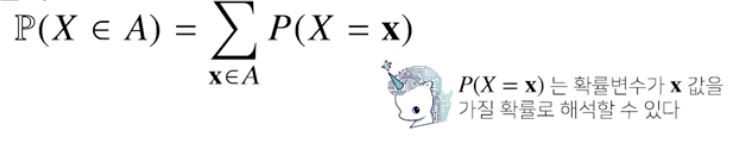
연속확률변수
데이터 공간에 정의된 확률변수의 밀도 위에서 적분을 통해 모델링한다.
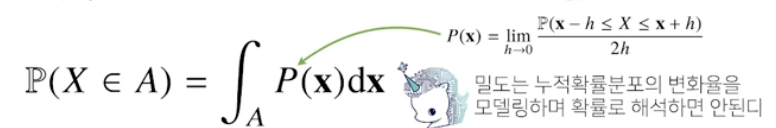
P(x) 라는 함수는 밀도 함수. 확률이 아니라 누적확률분포의 변화율이다.
이산확률변수도, 연속확률변수도 아닌 두가지의 혼합형도 존재한다.
주변확률분포
“주변확률분포”란, 다변수 확률분포에서 일부 변수의 값을 고려하지 않고 다른 변수의 분포만을 나타내는 확률분포를 말합니다. 예를 들어, 두 변수 (X)와 (Y)의 결합 확률분포가 주어졌을 때, (X)의 주변확률분포는 (Y)의 값을 고려하지 않고 (X)만의 분포를 나타냅니다. 이는 (Y)에 대한 모든 가능한 값에 대해 (X)의 확률을 합산하여 구할 수 있습니다.
조건부확률분포
조건부 확률분포는 특정 사건이 일어난 조건 하에서 다른 사건의 확률분포를 나타내는 개념입니다. 이를 통해 어떤 사건 ( B )가 주어졌을 때, 사건 ( A )의 확률을 어떻게 수정해야 하는지를 알 수 있습니다.
조건부확률과 기계학습
P(y|x) = 입력변수 x에 대해 정답이 y일 확률
Logistic Regression에서 선형모델과 softmax의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용한다.
조건부확률 P(y|x)를 구하는 방법
- 분류 문제에서 softmax(WΦ + b)는 데이터 x로부터 추출된 특징패턴 Φ(x)과 가중치 행렬 W를 통해 계산
- P(y|x) 대신 P(y|Φ(x))라 해도 무방.
딥러닝
- NN을 통해 데이터로부터 특징패턴 Φ를 추출.
'[Project_하다] > [Project_공부]' 카테고리의 다른 글
| [우리FISA] 2일차 Python basics with Colab (0) | 2024.07.09 |
|---|---|
| [우리FISA] 1일차 Orientation (0) | 2024.07.08 |
| [혼공컴운] CS기초, 입문 (0) | 2024.07.06 |
| [3Blue1Brown] Attention (1) | 2024.07.05 |
| [3Blue1Brown] Generative Pre-trained Transformer (0) | 2024.07.04 |
| [3Blue1Brown] Backpropagation 역전파 (0) | 2024.07.04 |
| [3Blue1Brown] DeepLearning (1) | 2024.07.01 |
Comments




